2024内蒙古公务员行测备考技巧:轴对称考点
小学二年级的数学课本中,我们学习了轴对称这一知识点,万万没想到大学毕业竟然还要学习轴对称。简单地做个回顾,所谓轴对称图形,即在平面内,一个图形沿一条直线折叠,直线两边的部分能够完全重合的图形叫做轴对称图形。这条直线叫做对称轴。
小学觉得简单的轴对称,在行测判断的图推当中可没有那么简单,有的同学看不出是轴对称的考点,有的同学就算看出是轴对称的考点但是却做不出题目。第一类同学的问题在于不知如何识别轴对称这类题型,第二类同学的问题在于不知轴对称这类题型有什么考点。接下来,将会从轴对称的题型识别和轴对称常考考点两个方面来讲解。
1.轴对称的题型识别
不得不说,轴对称在我们的生活中随处可见,大到国家级的建筑,如故宫、天坛、天安门等等,小到生活中的垃圾桶、书本、眼镜等等。虽然这是一个数学概念,但轴对称的物品、建筑,能够给人一种“安静”的严肃美、平衡美。因此,轴对称的图形往往看起来十分规整,这也就是轴对称题型的识别特征。虽然组成元素各不相同,但整体上来看,图形具有宏观的共性——规整。
2.轴对称常考考点
以小学学习到的画对称轴为基础,对称轴常考的考点有:①轴数量;②轴方向;③轴与线;④轴关系。我们逐一进行讲解
①轴数量,顾名思义,单纯的数轴的数量即可,轴数量可能构成常数数列(如1、1、1……)、等差数列(如1、2、3……;2、4、6……)、周期数列(如1、2、1、2……)、等比数列(如1、2、4……);
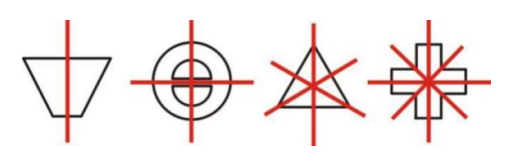
②轴方向,也就是在画出图形的对称轴以后,观察对称轴方向的变化,可能一组图形的对称轴都是水平方向的、或都是竖直方向的、或都是倾斜方向的;也可能发生旋转,旋转的角度也可能有所不同,比如每一次都是45°(即角度的变化构成常数数列),或是45°、90°、135°……(即角度的变化构成等差数列),或是45°、90°、45°、90°……(即角度的变化构成周期数列);

③轴与线,就是在画出图形对称轴的基础上,观察对称轴和图形原有线条是否出现重合,个别题目也会观察对称轴和图形的交点、顶点等是否出现重合;

④轴关系,与前面几个考点不同,这里的轴关系,主要指的是两个以上图形拼合在一起,无法整体观察对称轴,只能分别画出各个小图形的对称轴,再去观察各个图形的对称轴的关系,比如是否是平行关系、是否是垂直关系。

对称轴的考法比较灵活,这里只是跟大家简单的介绍了一些常考的题型。所以各位小伙伴在做题的时候,一定要先把图形的所有对称轴都一一画出,然后再去观察具体有什么样的规律。相信大家都能熟记对称轴的两个要点,并通过练习应用于题目中。














