2024国家公务员行测备考:利用几何特性巧解相似图形问题
在公务员考试中,行测和申论同样重要,而在行测中,数量关系可能是很多同学放弃的一部分。一方面大家对于数量关系或多或少存在畏难情绪,另一方面考试时间有限,很多同学做到数量的时候已经快要交卷了,于是大部分人放弃了这一部分。然而近几年在国考和部分省考中,数量关系的题目有简单易做的趋势,建议各位考生抓住数量关系中的基础知识点,才能做到解题游刃有余。
几何问题在国考和省考联考中是出现频率较高的一类题型,很多同学对几何问题几乎是望而却步,尤其是碰到立体图形的几何问题。虽然我们在高中阶段学了几个学期的几何,但在行测中的几何问题,是没有高中阶段那么难的。在行测中的几何问题里,经常会有一类题型,就是出现相似图形,那么对于解相似图形的问题,只要我们掌握了尺度扩大理论,就会迎刃而解了。
先让我们了解一下什么叫尺度扩大理论。先来举几个小例子:
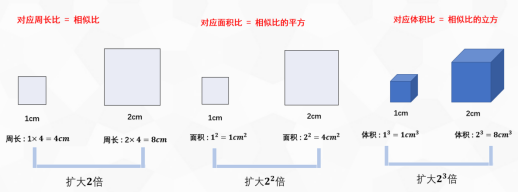

通过上图我们发现,在平面图形中,一个图形扩大n倍,那么周长也扩大n倍,面积扩大倍;对于立体图形,一个图形扩大n倍,表面积扩大倍,体积扩大倍。根据这一理论,我们在做几何问题时,碰到相似图形问题,都可以考虑使用这一理论,就能够做到快速解题。那么接下来让我们看几道例题来巩固一下:
【例1】如果一个圆的直径缩短20%,那么这个圆的面积缩小:
A.18% B.20%
C.36% D.40%
一个圆直径缩短,其还是一个圆,任意一个圆都可以看成相似图形,所以符合可利用尺度扩大理论。直径缩短20%,也就还剩80%,原来是100%,所以变化前后直径之比为![]() ,根据一个图形扩大n倍,面积扩大倍可知,变化前后面积之比为
,根据一个图形扩大n倍,面积扩大倍可知,变化前后面积之比为![]() ,则缩小了
,则缩小了![]() 。因此,本题选择C选项。
。因此,本题选择C选项。
这是一道平面几何问题,接着再让我们看一道立体几何问题。
【例2】将一个圆锥横向切开,切完后上下两部分的体积之比为1∶7,则切完后上半部分圆锥的底面直径是原来的( )倍。
A.0.4 B.0.5
C.0.6 D.0.8
根据圆锥横向切开,可得上部分与整个圆锥体相似,切完后上下两部分的体积之比为1∶7,则上部分与整个圆锥的体积之比为1∶8,根据尺度扩大理论可知,一个图形扩大n倍,体积扩大倍,1∶8即1∶,因此切完后上半部分圆锥的底面半径与整个锥体的底面半径之比为1∶2,即直径之比,因此切完后上半部分底面直径变为原来的0.5倍。因此本题选择B选项。
总结一下,当我们在做数量关系时,读题发现几何问题中有相似图形时,可以考虑用尺度扩大理论。这样,碰到相似图形问题我们就能够不慌张、迅速解题了。下面为大家整理了几何问题中尺度扩大理论的思维导图,大家可以保存收藏。
















