1.(单选题)某公司有三个部门,第一个部门的人数是其他两个部门人数的三分之一,第二个部门的人数是其他两个部门人数的五分之一,第三个部门有35人。则第一个部门与第二个部门人数相差多少?( )
A.4
B.5
C.6
D.8
解析
解法一:
第一步,本题考查基础应用题。
第二步,第一个部门的人数是其他两个部门人数的三分之一,说明第一个部门的人数与其他两个部门人数的比为1∶3,即总人数是4的倍数;同理,第二个部门的人数是其他两个部门人数的五分之一,说明第二个部门的人数与其他两个部门人数的比为1∶5,即总人数是6的倍数。
第三步,设总人数为24x,则第一个部门的人数为6x、第二个部门的人数为4x、第三个部门的人数为24x-6x-4x=14x,由于第三个部门有35人,可得14x=35,x=2.5。
第四步,第一个部门与第二个部门的人数相差6x-4x=2x=2×2.5=5(人)。
因此,选择B选项。
解法二:
第一步,本题考查基础应用题。
第二步,设第一个部门的人数为x、第二个部门的人数为y,由题意列式3x=y+35、5y=x+35,解得x=15、y=10。
第三步,第一个部门与第二个部门的人数相差15-10=5(人)。
因此,选择B选项。
2.(单选题)一次会议某单位邀请了10名专家,该单位预定了10个房间,其中一层5间、二层5间。已知邀请专家中4人要求住二层,3人要求住一层,其余3人住任一层均可,那么要满足他们的住房要求且每人1间,有多少种不同的安排方案?
A.43200
B.7200
C.450
D.75
解析
第一步,本题考查排列组合问题,属于基础排列组合。

第三步,总安排方案有120×60×6=43200(种)。
因此,选择A选项。
3.(单选题)有120名职工投票从甲、乙、丙三人中选举一人为劳模,每人只能投一次,且只能选一个人,得票最多的人当选。统计票数的过程中发现,在前81张票中,甲得21票,乙得25票,丙得35票。在余下的选票中,丙至少再得几张选票就一定能当选?
A.15
B.18
C.21
D.31
解析
解法一:
第一步,本题考查最值问题,属于最不利构造,用固定套路解题。
第二步,考虑最不利情况为丙与第2名乙的票数相等,设剩余的120-81=39(张)票中丙获得x张,乙获得(39-x)张,最不利情况为35+x=25+39-x,解得x=14.5。
第三步,为了保证丙要当选,至少再得15张票。
因此,选择A选项。
解法二:
第一步,本题考查最值问题,属于最不利构造。
第二步,在前81张票中,丙领先第二名乙35-25=10(张)票,故在剩下的120-81=39(张)票中,首先分配10张给乙,还剩29张。丙要保证一定当选,则应该获得剩余票量的半数以上,即至少15张。
因此,选择A选项。
解法三:
第一步,本题考查最值问题,属于最不利构造。用代入排除法解题。
第二步,代入A,则丙票为35+15=50,剩余票量39-15=24,即使全给威胁最大的乙,乙得25+24=49,小于丙,满足条件。
因此,选择A选项。
4.(单选题)将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料,然后将其切成64个棱长1厘米的小正方体,再用这些小正方体堆成棱长4厘米的大正方体,且使黑色的面向外露的面积要尽量大,问大正方体的表面上有多少平方厘米是黑色的?
A.88
B.84
C.96
D.92
解析
第一步,本题考查几何问题,属于立体几何类。
第二步,类似切割重构问题,分别从角(顶点)、棱和面三个维度进行讨论。原长方体中,角(顶点)处的小正方体,有4个面被涂色,棱上小正方体的3个面被涂色,剩余面上小正方体的两个相对面被涂色。
第三步,为了让新正方体黑色的面积尽可能大,则让小正方体黑色的面尽量外露。原长方体和新正方体的匹配过程如下表。

第四步,根据“角”位置比原来少4个小正方体,可得缺少黑色面3×4=12(个),用原来“面”位置多出的4个小正方体,放置在“角”位置,可看到黑色面有1×4=4(个),这样总共会缺少黑色面12-4=8(个)。由于每个面的面积为1平方厘米,故正方体黑色面积为4×4×6-1×8=88(平方厘米)。
因此,选择A选项。
5.(单选题)有一块三角形菜地如下图,现计划将其分为四块区域种植不同蔬菜,如果BE=3EC,AF=2EF,三角形BEF和三角形AFC的面积之差为10平方米,则三角形ABC的面积为:
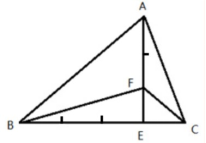
A.100平方米
B.120平方米
C.140平方米
D.150平方米
解析
第一步,本题考查几何问题,属于平面几何类。
第二步,设三角形FEC的面积为a。由题意可知,三角形 FBE和三角形FEC同高、底之比为3:1,则面积之比也为3:1,则三角形 FBE的面积为3a。同理,三角形 FAC和三角形FEC同高、底之比为2:1,则面积之比也为2:1,则三角形 FAC的面积为2a。三角形BFC和三角形AEC的面积之差也为10平方米,即3a-2a=10,解得a=10平方米。三角形ABF与三角形BEF同高、底之比为2:1,则面积之比也为2:1,故三角形ABF面积为2×3a=60平方米。
第三步,三角形ABC的面积为60+3a+2a+a=120平方米。
因此,选择B选项。
6.(单选题)某服装店老板去采购一批商品,其所带的钱如果只买某种进口上衣可买120件,如果只买某种普通上衣则可买180件。现在知道,最后该老板买的进口上衣和普通上衣的数量相同,问他最多可以各买多少件?
A.70件
B.72件
C.74件
D.75件
解析
第一步,本题考查基础应用题,用赋值法解题。

因此,选择B选项。
7.(单选题)某次圆桌会议共设8个座位,有4个部门参加,每个部门2人,排座位时,要求同一部门的两人相邻,若小李和小王代表不同部门参加会议,则他们座位相邻的概率是:
A.1/48
B.1/24
C.1/12
D.1/6
解析
解法一:第一步,本题考查概率问题。

解法二:第一步,本题考查概率问题。

8.(单选题)某五金加工厂一周加工的五金零件的统计表破损了,如图所示,表中缺少几个数字。根据这张统计表,星期五加工的零件数比星期六()。

A.多25件
B.少15件
C.多5件
D.少5件
解析
第一步,本题考查基础计算问题。
第二步,除星期五和星期六外,其余五天的零件加工数与平均值差(-12)+2+1+8+(-6)=-7,则星期五和星期六共加工75×2+7=157(件)。星期六尾数为6,可知星期五尾数为1,即星期五加工了71件,星期六加工了157-71=86(件)。星期五加工的零件数比星期六少15件。
因此,选择B选项。
9.(单选题)A、B、C三支施工队在王庄和李庄修路,王庄要修路900米,李庄要修路1250米。已知A、B、C队每天分别能修24米、30米、32米,A、C队分别在王庄和李庄修路,B队先在王庄,施工若干天后转到李庄,两地工程同时开始同时结束。问B队在王庄工作了几天?
A.9
B.10
C.11
D.12
解析
第一步,本题考查工程问题,属于条件类。
第二步,设两地工程同时结束的时间为t天,有1250+900=(24+30+32)×t,解得t=25。
第三步,设B队在王庄干了x天,根据题意有24×25+30x=900,解得x=10。
因此,选择B选项。
10.(单选题)某天,林伯的水果摊三种水果的价格分别为:苹果6元/斤,芒果5元/斤,香蕉3元/斤。当天,苹果与芒果的销售量之比为4︰3,芒果与香蕉的销售量之比为2︰11,卖香蕉比卖苹果多收入102元,林伯这天共销售三种水果()斤。
A.75
B.94
C.141
D.163
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设芒果销售了6x斤,则根据比例苹果销售了8x斤,香蕉销售了33x斤。由题意,得:3×33x-6×8x=102,解得x=2,故三种水果共销售8×2+6×2+33×2=94(斤)。
因此,选择B选项。














